 .
.
EE 643 Project #3 Spring 1997
This project will explore and compare various methods for designing IIR
filters.
There are 4 classical IIR filters and their
counterparts (1) Butterworth, (2) Chebyshev, (3) Chebyshev II, (4) elliptic
function. They represent four different combinations of two error approximation
measures. One error measure uses the Taylor series. This method equates as
many of the derivatives of the desired response as possible to those of
the actual
response. The other approximation minimizes the difference between the desired
and the actual response over a band of frequencies. The MATLAB analog
filter design programs all normalize the band edge to 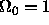 .
.
 .
This filter is also called maximally flat since it is optimal in the sense
that as many derivatives as possible equal zero at w=0 and
.
This filter is also called maximally flat since it is optimal in the sense
that as many derivatives as possible equal zero at w=0 and 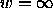 . The
formula for the magnitude squared of the normalized frequency response of an
Nth order analog Butterworth lowpass filter is given by
. The
formula for the magnitude squared of the normalized frequency response of an
Nth order analog Butterworth lowpass filter is given by
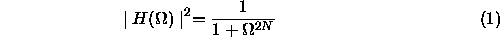
This response is normalized so that the magnitude squared is always 1/2 at
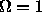 for any N. Replacing
for any N. Replacing  by
by 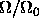 would
allow an arbitrary band edge at
would
allow an arbitrary band edge at 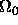 .
.
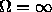 . The maximum error
over a band is called the Chebyshev error.
. The maximum error
over a band is called the Chebyshev error.
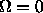 and has
minimum Chebyshev error in stop band. This is often a more practical
combination of characteristics than the usual Chebyshev filter.
and has
minimum Chebyshev error in stop band. This is often a more practical
combination of characteristics than the usual Chebyshev filter.
These four optimal analog filters can be transformed into optimal digital
filters with the bilinear transform that is investigated in the second half
of this project. The IIR filter design programs in MATLAB take care of
analog filter design and bilinear transformation into the digital form
automatically.
Exercises
Use the MATLAB command butter to design a 5th-order lowpass IIR filter with sampling frequency of 2 Hz and a band edge of 0.6 Hz. Plot the magnitude and phase frequency responses using freqz. Plot the pole and zero location diagram using zplane. Plot the significant part of the impulse response using filter to give around 20 output values. Discuss briefly how the magnitude response makes sense from the pole-zero plot.
Use the MATLAB command cheby1 to design a 5th-order lowpass IIR filter with a sampling frequency of 2 Hz, a band edge of 0.6 Hz, and a passband ripple of 0.5 dB. Plot the magnitude and the phase frequency responses. Plot the pole and zero location diagram. Discuss briefly how the magnitude response makes sense from the pole-zero plot.
Use the MATLAB command cheby2 to design a 5th-order lowpass IIR filter with a sampling frequency of 2 Hz, a band edge of 0.6 Hz, and a maximum stopband ripple 30 dB below the passband response. Plot the magnitude and the phase frequency responses. Plot the pole and zero location diagram. Discuss briefly how the magnitude response makes sense from the pole-zero plot.
Use the MATLAB command ellip to design a 5th-order lowpass IIR filter with a sampling frequency of 2 Hz, a band edge of 0.6 Hz, a passband ripple of 0.5 dB, and a maximum stopband ripple 30 dB below the passband response. Plot the magnitude and the phase frequency responses. Plot the pole and zero location diagram. Discuss briefly how the magnitude response makes sense from the pole-zero plot.
In what way(s) can the performance of these filters be compared since their specifications are not the same?
Do the impulse responses approximate the impulse response of an ideal lowpass filter? Explain.
The filtering specifications for a particular job had a sampling rate
of 2 Hz, passband ripple of 0.1 dB, passband edge of 0.28 Hz, stopband
edge of 0.32 Hz, and a stopband ripple below 30 dB. What order
Butterworth, Chebyshev, Chebyshev II, and elliptic filters will meet
these requirements? Use the butterord, cheb1ord,
cheb2ord, and
ellipord commands. Why does the elliptic filter have the lowest
order?
Read in the file /opt/demo/audio/doorbell.au using
auread.
Using the
fft function,
determine the frequencies of the upper and lower tone of the doorbell.
Design a filter such that the lower tone is attenuated no more than
3 dB while the upper tone is attenuated at least 15 dB. Design all
four types of filter. Listen to the filtered signal for each case.
Compare the results for each of the filters in terms of sound and
filter order.
What happens if you attempt to design and implement a Butterworth filter with passband attenuation less than 1 dB and stopband attenuation greater than 60 dB? Explain.
Write a short report describing your findings. The report should
contain a concise description of your results.
Include listings of your function. Be sure to answer all questions.
You are not expected to include in
the report all plots which you were required to do; instead, you should
summarize in your report the important features of the unincluded plots.
For further help: