Wide Temperature Range Compact Modeling (93-393K)

Background

One of the remarkable characteristics of SiGe HBT is the ability to operate over a wide temperature range, from as low as sub 1K, to as high as over 400 K. This, together with excellent total dose radiation tolerance, makes it very attractive for implementing space electronics that can operate over a wide temperature range in presence of radiation as found in space missions.

Recently, a research team led by Prof. John Cressler at Georgia Tech took on the challenge of developing SiGe electronics that can operate in extreme environments as found in many space missions as is, without warms boxes and radiation shields.

To enable such extreme electronics designs, and in collaboration with Prof. Cressler’s team at Tech and Prof. Mantooth’s team at Arkansas, my team developed new SiGe HBT compact model that can function from 43 to 393K. Existing design kit simply fails to run or give erroneous results outside its intended temperature range, typically from -50 C and +120 C (223 to 393K), making necessary development of wide-temperature range compact models.

Approach and Challenges

The effort turned out to be much more involved and harder than I had originally expected.

Our starting point was to take an existing SiGe HBT compact model, and modify the temperature scaling of model parameters to “fit” measurement data over a wider temperature range. However, we often find that a model parameter extracted at various temperatures does not show any physically meaningful temperature dependence. The parameters extracted for a given temperature are not unique, and several different parameters sets could all yield acceptable fitting. This is primarily the case at higher temperatures.

At lower temperature, we found that no matter what parameters we use at a given temperature, the model cannot possibly fit certain characteristics. This means that new model equations must be developed. Existing transistor theories may not be able to explain measured low-temperature characteristics, making empirical or semi-empirical equations necessary.

In modern SiGe HBTs, operating current density is on the order of mA per square micron, causing severe self-heating. The degree of self-heating is biasing current and voltage dependent. For extraction of high current model parameters, we had to deal with self-heating by accounting for known t-dependence functional form of all model parameters, which is how it is done in commercial compact modeling around room temperature. The situation is much worse in bipolar transistors compared to field-effect transistors, because bipolar transistors operate on the principles of minority carrier injection and diffusion, both are strongly temperature dependent. For extremely wide temperature range, we do not know what functional form a high current parameter t-dependence will take. We will need to assume a functional form, extract parameters over temperature, and then update the functional form iteratively.

As a result, extending T-scaling capability of a compact model is not as straightforward as simply extracting model parameters at different temperatures and construct new T-scaling equations for these model parameters.

We chose Mextram as basis of our model development, and made extensive new developments to enable wide temperature range modeling. All of the important cryo physics such as freeze-out and trap-assisted tunneling are accounted for.

Modeling Results

Below are the DC and AC modeling results from 393K down to 43K, from DC to 5GHz, over a wide range of biases of interest to circuit design, all with a single T-scalable model.

Gummel Plots

Figure 1 shows comparison of measured and modeled Gummel plots. A reasonable accuracy across temperature is achieved for all levels of injection. Trap-assisted tunneling is obvious below 93K and clearly needs to be accounted for. A high injection kink is clearly visible at nearly all temperatures and becomes more important with cooling. Modeling of the kink is closely related to the epi-layer quasi saturation model parameters (e.g. VDC) as well as the emitter resistance.

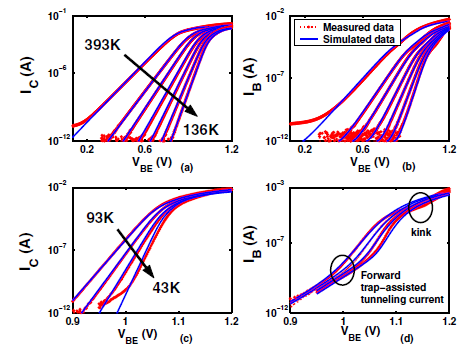
Figure 1: Gummel plots.

fT-IC

Figure 1 shows characteristics at . , 1 and 2V.

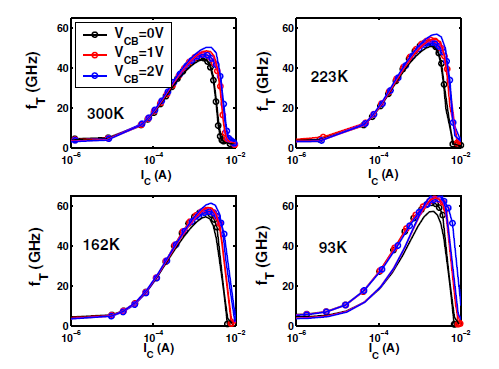
Figure 2: fT-IC plots.

Y-parameters vs IC

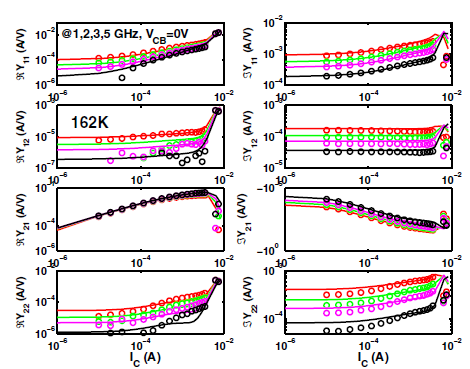
Figure 3: Y-IC plots.

Circuit Applications

Bandgap Reference

Precision bandgap references (BGRs) are extensively used in a wide variety of circuits required for wide temperature range operation. SiGe BGRs have shown excellent over temperature stability. The circuit is also an excellent candidate for validating a compact model in the low to medium injection region. Simulated and measured BGR output versus temperature is shown in Figure 4. The same transistors used in the measured BGR are used for model parameter extraction. The excellent agreement indicates the accuracy of the compact model.

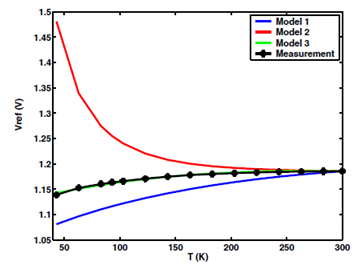
Figure 4: Bandgap reference circuit output voltage vs T plots.

Single-Event Upset Threshold LET

One important advantage of SiGe HBTs is the “free” total dose tolerance which holds at low temperatures as well. The bigger concern is single-event upset (SEU). Energetic particles passing through the junctions can deposit electron-hole pairs, which are then collected by transistor terminals. Such transient currents can cause problems to digital, analog and RF circuits. Of particular importance is the drift charge collection in the collector-base (CB) and collector-substrate (CS) junction. Even though the CB junction charge is not large in amount, it is not negligible and can be important for circuit SEU, simply because the charge collection current appears between the collector and base, a feedback position.

For a given Linear Energy Transfer (LET), which measures the number of electron-hole pairs deposited per linear distance of particle travel, CB and CS junction charge collection currents $I_{CB}$ and $I_{CS}$ are simulated using 3-D device simulation, and then fed into Cadence to determine circuit response. The LET at which an upset occurs is called threshold LET, and is used as an SEU figure-of-merit.

Simulated threshold LET vs temperature is given below for a master-slave D flip flop when the tail current is kept constant over temperature. Simulations were done with different combinations of the CS and CB transient SEU currents.

The results are shown in Figure 5. Threshold LET increases overall with cooling, which is certainly good news, as no additional SEU hardening is necessary for circuit operation at cryogenic temperatures.

Figure 5: Threshold LET vs T plots.