John Y. Hung

Quantization in Estimation and Control
Sensor value quantization and its effects have been examined for more than 55 years
by many researchers. A study of the classical research and textbook literature shows
that the issues and analysis methods fall into three general groups. Some researchers
have examined quantization using a worst case analysis, both in a dynamic sense and
in steady state. Bounds on the sampled quantization error in the output can also be
computed by finding the impulse response from the quantizer input to the system output.
As early as 1956, Widrow treated quantization error as a random process, and studied the
response of a linear system to a random process. For a random signal input, a common
stochastic model of quantization error is a white random process having uniform
probability density function. The stochastic model approach is very useful in
communication system problems. One of the most comprehensive compilations of research
about quantization has been written by Gray and Neuhoff, who traced the history of quantization
research and applications, starting from the 1948 seminal works of Oliver, Pierce, Shannon,
and Bennett.
In feedback control systems, signals tend to be more deterministic and exhibit stronger
correlation over time, so the stochastic modeling approach doesn't always predict
certain behaviors well. The noise model approach is not a good model in applications
where the signal is slowly varying or the quantization level is large. More recently,
both linear and nonlinear system analysis methods have been applied (Delchamps), with the latter
case treating the quantization characteristic as a nonlinearity with the view toward
predicting the periodic behavior (limit cycles) that can persist in feedback systems (Franklin,
Powell, and Workman).
Optimal filters such as the Kalman filter have been suggested as a measure to counteract
quantization effects.
Very recently, Brockett and Liberzon address feedback stabilization problems for linear
time-invariant control systems with quantized measurements. They propose a control design
approach that relies on the possibility of changing the sensitivity of the quantizer in
real time. When applied to systems that are stabilizable by linear time-invariant feedback,
their approach yields global asymptotic stability. Liberzon also derives a relationship
between the number of values taken by a sampling encoder and the norm of the transition
matrix of the open-loop system over one sampling period, and describes conditions that
guarantee global asymptotic stabilization.
Researchers are also studying the effects of sensor quantization on filtering and state
estimation. The earliest works treat the problem from a stochastic systems viewpoint.
For example, Curry proposed methods to design an optimal filter using a minimum variance
criterion. More recently, advances from the study of information theory have been examined
by Delchamps, who treats quantization as "partial observation" rather than approximation
of quantities. He suggest a feedback control technique to generate an input sequence
that yields additional information about the true state over a period of time. Along this
approach, Feng and Loparo model the quantized state as nonlinear partial observation of
the true state, and formulate the estimation problem as an entropy optimization problem
with an intepretation as an optimal control problem for a Markov chain. An optimal design
based on minimizing the entropy costs is proposed, but their results are restricted to
first-order systems. Sviestins and Wigren propose a set of nonlinear filters that
recursively estimate the state by propagating the state probablity density through the
Fokker-Planck equation. All of these methods consider first-order systems.
A Different Approach
Instead of the classical stochastic modeling approach, Auburn University co-investigators Hung and
A. S. Hodel
treat the measurement quantizer as a deterministic and memoryless nonlinearity pheneomena,
which lends the problem to Lyapunov-like analysis. In constrast to the recent advances from
information theory , a very simple method to counteract quantization effects is proposed.
If the input of the quantizer is known, then the output is deterministically known from the
quantizer model. In practice, the quantizer input is not perfectly known, but an estimate
is available. Since the quantizer error function is also known, that information can be used
to improve the estimate of the output. One method to improve on the estimator output would be
to apply the mathematical inverse of the error function, in a manner akin to feedback
linearizing control or nonlinear output injection. The sawtooth-shaped error functions of
the quantizer are not invertible at boundaries of the quantization level, but these points
are a set of measure zero. The proposed estimator modification does not require implementation
of the inverse function, however, because both the estimator state and estimator output are
accessible. Instead, the quantizer model is simply embedded in the observer structure, so
that the estimator output is quantized in the same way that the plant output is quantized.
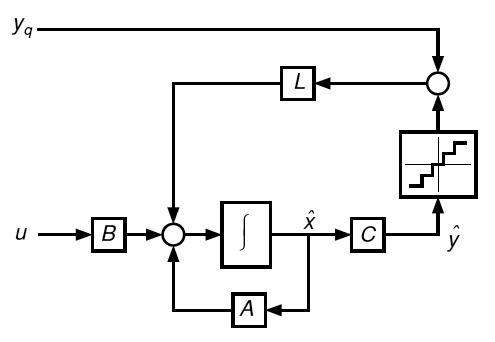
Fig. 1. Block diagram of the nonlinear state estimator incorporating quantizer.
Plant input u, quantized measurement y_q, estimator state x_hat.
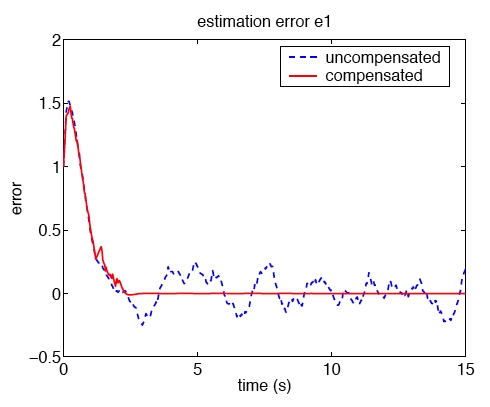
Fig. 2. Comparison of state estimation errors.
Related publications
-
J. Y. Hung,
"An output feedback controller with reduced sensitivity to sensor quantization,"
Proceedings of 2004 IEEE International Symposium on Industrial Electronics,
Ajaccio, FRANCE, May 2004.
-
A. S. Hodel and J. Y. Hung,
"An observer with reduced sensitivity to sensor quantization,"
Proceedings of 29th Annual Conference of IEEE Industrial Electronics Society,
Roanoke, VA, November 2003, pp. 586-590.

Back to John Hung's home page
Last updated 14 July 2005



