Three-dimensional particle image velocimetry with a plenoptic camera
- Student: Tim Fahringer
- Funding Agency: Air Force Office of Scientific Research
Experimentally quantifying the topology of unsteady coherent flow structures in turbulent flows remains at the forefront of fluid mechanics research. The inability of planar methods, such as particle image Velocimetry (PIV), to describe these phenomena can be directly attributed to their 2-D nature. An instantaneous fully three-dimensional (3-D), three component (3-C) velocity field would be instrumental in the quantification of turbulent flows. The goal of this research is the development of a novel technique capable of capturing the full 3-D, 3-C velocity field using the concept of light field imaging and tomographic reconstruction.
The term light field is used to describe the complete distribution of light rays in space, and can be described by a 4-D function, sometimes termed the plenoptic function. Each ray in the light field can be parameterized in terms of the plenoptic function as its position (x,y) and its angle of propagation (θ,φ). Light field imaging describes the methods and hardware used to capture the full light field. In contrast to conventional photography, which only captures the spatial distribution of the 4-D light field, light field photography can capture the full 4-D light field. One of several ways to capture the light field is to use a microlens array mounted near a CCD to encode this information onto a single sensor. This device, termed the plenoptic camera, is the focus of this work.
For this research the primary goal is to reconstruct3-D volumes of particles in order to perform cross-correlation based velocimetry analysis. To facilitate this, the algorithms and ideas developed in the field of optical tomography are utilized. Tomographic reconstruction is simply a reconstruction of a N-dimensional object from an (N-1)-dimensional data set, or reconstruction from projections. This technique is widely used in the field of medical diagnostics such as in PET, CT, CAT, and MRI scans. Mathematically the tomographic reconstruction problem is an inverse problem and can be expressed in the form: Ax = b. Where x is the object that is to be reconstructed, b is the given data set, and A is the projection operator that describes how b was obtained from x. For our unique application, the A matrix is determined using a unique 4-D light field interpolation scheme. The actual reconstruction process is done using the Multiplicative Algebraic Reconstruction Technique (MART), as it is the current standard in tomo-PIV.
|
|
|
|
Prototype Plenoptic Camera |
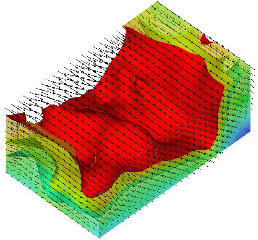
3-D vector field with streamwise velocity iso-surface of a turbulent boundary layer |
For more details, please see:
- Fahringer, T., Thurow, B., “The Effect of Grid Resolution on the Accuracy of Tomographic Reconstruction Using a Plenoptic Camera,” AIAA Paper 2013-0039, 51st AIAA Aerospace Sciences Meeting Dallas, Texas, January 2013
- Fahringer, T., Thurow, B., “Tomographic Reconstruction of a 3-D Flow Field Using a Plenoptic Camera,” AIAA Paper 2012-2826, 42nd AIAA Fluid Dynamics Conference and Exhibit New Orleans, Louisiana, June 2012
- Melnick, M., Thurow, B., Fahringer, T., Brock, B., “Experimental Investigation of Three-Dimensional Structures in an Adverse Pressure Gradient Turbulent Boundary Layer,” AIAA Paper 2012-2850, 42nd AIAA Fluid Dynamics Conference and Exhibit New Orleans, Louisiana, June 2012
- Lynch, K., Fahringer, T., Thurow, B., “Three-Dimensional Particle Image Velocimetry Using a Plenoptic Camera,” AIAA Paper 2012-1056, 50th AIAA Aerospace Sciences Meeting Nashville, Tennessee, January 2012